III Les Fractales : définition, propriétés
1°. Annonce générale
de la définition d'une fractale et de ses propriétés
Le mot "fractal" devenue
"fractale" par abus de langage, a été formé pour
la première fois dans les années 1970 par MANDELBROT Benoît
à partir du latin "fractus" qui signifie "brisé".
Une fractale, qui correspond à une forme géométrique particulière,
possède plusieurs caractéristiques qui en font des "bizarreries
de la nature" tout à fait stupéfiantes :
. Ses
parties ont la même forme, la même structure que l'objet tout entier
hormis le fait qu'elles se trouvent à des échelles différentes
(de l'infiniment petit à l'infiniment grand) et qu'elles peuvent être
trés légèrement modifiées.
. Sa forme est extrêmement
irrégulière, abondamment fracturée en tout point (d'où
son origine éthymologique...) et ce quelle que soit l'échelle
où on l'observe : aussi bien de l'infiniment petit à l'infiniment
grand.
. Sa dimension, appelée
dimension fractale, n'est en règle général pas un nombre
entier mais un nombre fractionnaire contrairement à la plupart des objets
et des formes que nous connaissons.
. Enfin, et c'est bien là l'une de ses propriétés les plus stupéfiantes : une fractale possède une aire finie pour un périmètre...infini !!!
2°. Démonstration des deux propriétés les plus surprenantes : celle de l'aire finie pour un périmètre infini
Nous allons démontrer ces propriétés sur un exemple concret : celui du flocon de Von Koch dont le principe de construction, bien plus détaillé dans la partie "les différents ensembles fractales", figure ci-dessous.
En réalité, seul un côté de notre flocon (qui correspond à l'origine à un triangle équilatéral) est étudié ici. Pour passser de l'itération 0 (celle tout en haut) à l'itération 1, il suffit de diviser la longueur de notre côté en 3, puis il faut ôter le 1/3 central pour le remplacer par 2 segments identiques au segment ôté afin de former un triangle équilatéral (qui a donc pour base 1/3 du segment d'origine).
Considèrons donc le flocon de Von Koch au bout de n itérations.
a) Démonstration
du périmètre infini du flocon de Von Koch
Soit U(n) le nombre de côtés au
rang n ; c'est à dire au bout de n itérations. On a donc
U(n) = 3 x 4^n (3 côtés initiaux à l'origine,
pour chacun d'entre eux, de la formation de 4 nouveaux côtés et
ce pour chaque rang).
Soit V(n) la longueur d'un côté.
En prenant 1 pour longueur du premier côté, nous avons donc v(n)
= 
(pour chaque itération,
le côté précédent a sa longueur divisée par
3).
Soit P(n) le périmètre
du flocon, nous avons donc : P(n) = 3 x 4^n x
<===> P(n) = 3 x 
Comme 4/3 > 1, alors
on peut en déduire que : 
P(n) =
3 x = 
Nous pouvons donc en déduire, au vue des résultats, que le flocon de Von Koch possède un périmètre infini ; ce qui justifie une partie des propriétés que nous avons attribuées aux fractales.
b) Démonstration de l'aire finie du flocon de Von Koch
Soit S(n) l'aire
de notre flocon au bout de n itérations. On démontre facilement
(à l'aide de la propriété de Pythagore) qu'un triangle
équilatéral de base a a pour aire 
.
La suite S(n) est définie
par :
L'aire au rang n+1 correspond
en effet à l'aire au rang n [= S(n)] à laquelle on doit ajouter
la nouvelle aire qui correspond au nombre de côtés précédent
(car chaque côté précédent va être à
l'origine de la formation d'un triangle) U(n) multiplié par l'aire engendrée
par la formation d'un nouveau triangle équilatéral de base V(n+1).
Cette première étape ayant été effectuée avec succès, nous allons poursuivre notre démonstration en exprimant désormais S(n) en fonction de n:
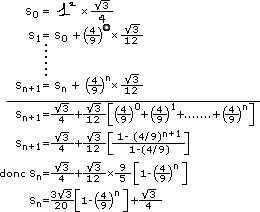
La première étape
de cette série de calculs (jusqu'au trait de séparation) consiste
à sommer membre à membre tous les termes entre eux. On remarque
en effet que les termes S(...) s'annulent 2 à 2 sauf S(o) et S(n+1) qui
sont "uniques". Suite à une factorisation trés simple,
nous obtenons donc la première ligne de calcul qui suit le trait de séparation.
Le passage à la deuxième
suite se fait grâce à l'utilisation d'une propriété
sur les puissances que nous avons vue en cours de spécialité :
en posant x = (4/9), nous avons en effet (1 + x + x^2 + ... + x^n)
= [1 - x ^ (n + 1)] / (1 - x) . C'est exactement cette propriété
qui a été utilisée ici.
Ainsi, nous arrivons à
la fin de ce laborieux calcul. Déterminons désormais la limite
de cette suite :
S(n) = 
car comme (4/9) < 1,
(4/9)^n = 0
d'où,
après simplification des fractions,
S(n) =
Nous pouvons donc en déduire, au vue des résultats, que le flocon de Von Koch possède une aire finie ; ce qui justifie une autre partie des propriétés que nous avons attribuées aux fractales.