IV La Dimension Fractale

   1°. Introduction à la notion de dimension

      Dans notre environnement au quotidien, nous connaissons tous des objets à 1 dimension (comme une ligne, une corde tendue, un fil de fer…), à 2 dimensions (une feuille de papier dotée d'une longueur et d'une largeur) ou encore à 3 dimensions (par exemple un bloc avec hauteur, longueur et largeur) ; la 4ème dimension faisant référence au temps qui s'écoule.

      En fait, la notion mathématique de dimension fait référence au nombre de vecteurs composant une base d'un espace vectoriel et peut s'interpréter intuitivement en terme de positionnement spatial comme le nombre minimal de déplacements standarts en lesquels peut se décomposer un déplacement quelconque. C'est ainsi qu'un point, à l'intérieur duquel il est impossible de se mouvoir, est de dimension 0 (aucun vecteur de déplacement). De même, une droite, sur laquelle on ne peut que glisser, est de dimension 1 (1 seul vecteur de déplacement), un plan est de dimension 2 car on peut se déplacer librement sur la surface de celui-ci (2 vecteurs de déplacement) et l'espace physique qui nous entoure est de dimension 3 dans la mesure où nous pouvons nous y déplacer " en long, en large et en travers " (3 vecteurs de déplacement). Le tableau qui suit récapitule ces différentes dimensions avec leur unité de mesure respective :

   2°. Problèmes liés à la dimension fractale

     La notion de dimension paraît donc à première vue assez simple ; et pourtant il n'en est rien…Quelle est par exemple la dimension d'une feuille de papier froissée ? La boulette, absolument irrégulière et imparfaite a une hauteur variable en tout point : nulle par endroits et digne d'un volume en d'autres localités. La dimension d'un tel objet ne peut pas être un nombre entier (0, 1, 2 ou 3) puisque cette boulette ne correspond fondamentalement ni à un point, ni à une droite, ni à une surface, ni à un volume. Sa dimension est donc un nombre compris entre 2 et 3 (car cette boulette se rapproche le plus d'un " mixte " entre une surface et un volume).

      Ce sont bien entendu des mathématiciens à l'esprit de contradiction qui ont pour la première fois soulevé ce problème : ceux-ci cherchaient en effet, comme à leur habitude, le grain de sable qui grippait la machine. Cette bizarrerie, qui échappe encore aujourd'hui largement au commun des mortels (il est en effet difficile de s'imaginer qu'un objet puisse avoir une dimension comprise entre 2), a inspiré plusieurs férus de géométrie dont notre cher Benoît Mandelbrot qui voit dans les fractales la clef de cette bizarrerie : toutes les fractales (ou presque) présentent en effet la caractéristique de posséder une dimension non entière comme la boulette de papier par exemple ; nous l'avons certes dit précédemment ; mais attardons nous désormais à le démontrer.

   3°. Explication d'une méthode pour évaluer la dimension d'un objet

     Pour calculer la dimension de certains objets, nous allons utiliser la méthode suivante : nous allons prendre un étalon de cet objet, c'est à dire cet objet lui même mais en plus petit (= une portion de l'objet d'origine) , et nous allons reporter cet étalon sur notre objet d'origine un certain nombre de fois. Nous allons réaliser cette opération pour deux "objets" différents : un segment puis un carré ; et nous généraliserons par la suite les résultats obtenus.

     a) Pour le segment

     Soit L la longueur totale de notre segment. Nous allons prendre un étalon de longueur n de ce segment que nous allons reporter sur ce même segment un certain nombre de fois : (L/n) fois plus précisément. On remarque alors que (L/n) = (L/n)^1  

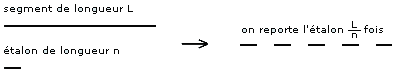
      b) Pour le carré

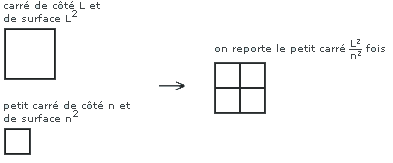
     Soit L^2 la surface totale de notre carré. Cette fois, nous prenons un autre carré plus petit de côté n et de surface n^2. Nous allons reporter le petit carré sur le grand, tout comme nous l'avons fait pour le segment. Ce petit carré sera ainsi reporté (L^2/n^2) fois pour obtenir la surface du grand carré. On remarque alors que (L^2/n^2) = (L/n)^2

     c) Généralisation de la notion de dimension

     Dans ces deux exemples, nous avons fait apparaître le nombre 1en exposant pour le segment, et le nombre 2 pour le carré. Ces nombres sont, par convention, la dimension de l'objet.
    
      Généralisons : soit N le nombre de fois que l'on reporte l'étalon de longueur n sur notre objet de longueur L, et soit d la dimension de l'objet. On a donc N = (L/n)^d
     
      Or,        N = (L/n)^d
      <===> ln N = ln ((L/n)^d)
      <===> ln N = d * ln (L/n)
      <===> d = ln N / ln (L/n)                                                        On a donc pour récapituler :

     d) Vérification de cette formule sur un exemple simple : celui du cube

     Considérons un cube de 2 cm de côté et un autre de 1 cm de côté. Il faut ainsi 8 cubes de 1cm de côté pour remplir un cube de 2 cm de côté (puisque un cube de 2 cm de côté a un voulume de 8cm3 et un cube de 1cm de côté a un volume de 1cm3). Nous possédons donc les données suivantes :
                 n (longueur du côté de notre petit cube) = 1
                       L (longueur du côté de notre grand cube) = 2
                       N (nombre de fois que l'on reporte le petit cube sur le grand cube) = 8

     Ainsi, grâce à notre magnifique formule présente juste au dessus, nous allons pouvoir calculer la dimension d'un cube (bien que nous connaissions par avance le résultat) :            d = lnN / ln (L/n)
                                                                              d = ln 8 / ln (2/1)
                                                                              d = ln 8 / ln 2
                                                                              d = 3
     Le résultat obtenu par cette formule est ainsi bien conforme au résultat attendu : la dimension d'un cube est en effet 3

     e) Application de cette formule sur l'exemple du flocon de Von Koch

Rappel : Seul un côté de notre flocon (qui correspond à l'origine à un triangle équilatéral et qui possède donc 3 côtés) est étudié ici. Pour passser de l'itération 0 (celle tout en haut) à l'itération 1(celle juste en dessous), il suffit de diviser la longueur de notre côté en 3, puis il faut ôter le 1/3 central pour le remplacer par 2 segments identiques au segment ôté afin de former un triangle équilatéral (qui a donc pour base 1/3 du segment d'origine).

    Ainsi, si nous prenons comme longueur 1 pour le côté initial, nous avons :
                                                                                 n (longueur de notre étalon, c'est à dire de notre petit segment) = 1/3
                                                                                 L (longueur de notre grand segment) = 1
                                                                                 N (nombre de fois que l'on reporte le petit segment sur le grand segment) = 4

     D'où, grâce à notre formule précédente,      d = lnN / ln (L/n)
                                                                                d = ln4 / ln (1/(1/3))
                                                                                d = ln4 / ln 3
                                                                                d = 1,26 environ

     Nous pouvons donc en déduire que le flocon de Von Koch n'a pas une dimension entière mais une dimension fractionnaire environ égale à 1,26.

Page précédente                                                                                                                                                                                              Page suivante