VI Fabrication de fractales
Au cours de notre T.P.E., nous avons cherché à consrtruire certaines fractales qui figurent, pour la plupart, dans la partie "les différents ensembles fractales". Certaines ont été faites sur une feuille, d'autres en "3 dimensions" à partir d'une feuille et d'autres, enfin, par informatique grâce au logiciel Microsoft Excel. Nous avons sélectionné les meilleures que vous pouvez observer ci-dessous.
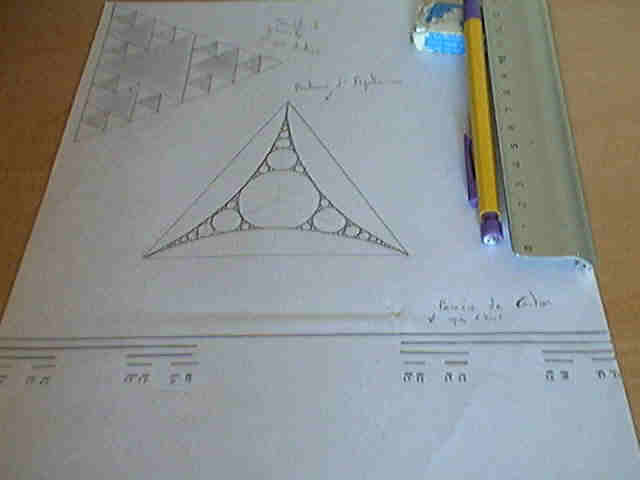
1°. Fractales en "2D" : Triangle de Sierpiensky (3 itérations), Baderne d'Apolonius et Poussière de Cantor (6 itérations)
Ces trois fractales ont été réalisées par nous-mêmes, à notre domicile, sur une feuille de papier blanc format A4 selon les principes énoncés dans la partie "les différents ensembles fractales". Elles sont trés simples à réaliser et trés agréables à regarder. Le Triangle de Sierpiensky figure en haut à gauche, la Baderne d'Apolonius au centre et la Poussière de Cantor en bas de la feuille.

2°. Pliage Fractale
Les deux fractales qui sont présentées ci-dessous ont été réalisées par nous-mêmes au C.D.I. et ce à partir de pliages successifs détaillés dans le hors-série "Tangente" n°18 sur les "Fractales". Leur forme en trois dimensions, aussi surprenante soit-elle, nous servira de support pour notre Cd rom lors de la présentation orale ; le site ne pouvant pas être mis sur internet pour cette date.
3°. Fractale assistée par ordinateur
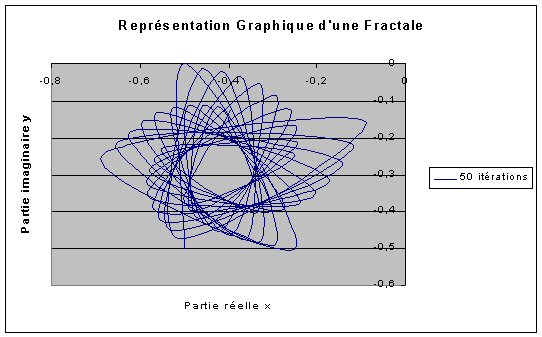
Il existe toute une série d'objets fractals curieux qu'il est possible de construire à partir d'opérations simples de la géométrie. Certains sont des figures planes, d'autres déploient leur structure dans l'espace comme celles vues précédemment. Mais si l'on applique le procédé d'itération à des formules utilisant les nombres complexes, on entre dans un monde fabuleux de formes étranges et d'une beauté parfois étonnante. Les calculs engendrés par ces formules ont été réalisées par ordinateur et ont ensuite été représentés sur un graphique. Pour comprendre comment nous avons fait, il faut lire les quelques lignes qui suivent...sinon descendez directement au bas de la page pour observer les résultats.
a) Qu'est-ce qu'un nombre complexe
C'est la première
question à laquelle il faut avoir une réponse si l'on veut créer
une fractale à partir de formules. Ainsi, un nombre complexe est un nombre
à la structure générale suivante : z = x + iy
Dans cette équation x et y représentent des nombres
réels et i est la racine carrée de -1 (par convention, on dit désormais
que i^2 = -1). x est appelé partie réelle du nombre et iy partie
imaginaire du nombre.
b) Fonction fractale
Prenons l'équation
z' = z^2 + c
Dans ce genre d'équations, c est un nombre
complexe quelconque fixé au départ sous la forme (c = x + iy).
On fait le calcul pour chacun des points z du plan complexe (chaque point a
une coordonnée x réelle et une coordonnée y imaginaire). Seulement, au lieu
de faire le calcul une seule fois pour chaque point, on recommence en donnant
à z la valeur z' trouvée dans le calcul précédent et l'on recommence encore
en donnant à z la valeur z' trouvée par ce nouveau calcul... En bref on effectue
un calcul par récurrence avec un nombre d'itérations théoriquement infini lors
du calcul de chacun des points. Cette relation de récurrence peut s'écrire
sous la forme suivante : z (n+1) = z(n)^2+c
En partant d'une valeur initiale z (0,0)
du plan complexe il est intéressant d'observer le comportement de cette suite
complexe pour chacun des points du plan complexe. On s'aperçoit que pour certains
points (c'est-à-dire de valeurs initiales de z) la fonction diverge plus ou
moins rapidement (la valeur de z' s'écarte de plus en plus de la valeur initiale).
Au contraire, pour certains autres points, les résultats restent définitivement
enfermés dans un intervalle limité.
c) Comment représenter graphiquement une fonction utilisant des nombres complexes?
Pour représenter
une fonction fractale il suffit de graduer les axes des abscisses et des ordonnées
normalement. Quand on gradue un axe de coordonnées on peut donner à chaque division
de l'axe une valeur d'unité conventionnelle quelconque. Si l'on dit que la valeur
d'une division vaut u pour l'axe des abscisses, on aura d'un côté de l'origine
la représentation des nombres u, 2u, 3u... et de l'autre côté -u, -2u, -3u...
Ensuite, une fois les axes gradués, on représente la partie imaginaire
du nombre trouvé (c'est à dire la partie ayant pour facteur i) sur l'axe des
ordonnées et la partie réelle (la partie ne comportant pas de i) sur l'axe des
abscisses.
L'axe des x représente donc la partie réelle
du résultat du calcul ; et l'axe des y représente la partie imaginaire.
d) Notre équation
Intéressons-nous
désormais à notre équation de fractales.
z = x + iy (avec x et y réels
qui varient) avec z(o) = 0
c = x' + iy' ( avec x' et y'
réels fixés)
Notre équation
générale est z(n+1) = z(n)^2 + c où n représente
le rang auquel nous nous trouvons et où n+1 représente donc le
rang suivant.
Nous avons donc au rang 1,
z(0+1) = z(0)^2 + c
=
0^2 + (x' +i y')
z(1)
= x' + iy'
Au rang 2 nous obtenons, z(1+1)
= z(1)^2 + c
=
(x' + iy')^2 + (x' + iy')
=
x'^2 + 2ix'y' + i^2y'^2 + x' + iy'
=
x'^2 + 2ix'y' - y'^2 + x' + iy'
z(2)
= x'^2 - y'^2 + x' + i(2x'y' + y')
Et ainsi de suite jusqu'à l'infini...
Ensuite, il faut séparer
la partie réelle (au rang 2 : x'^2 - y'^2 + x') et la partie imaginaire
(au rang 2 : i(2x'y' + y')) et il faut replacer les points obtenus dans le plan
complexe (la partie réelle correspond à l'axe des abscisses et
la partie imaginaire à l'axe des ordonnées).
L'ensemble des points qui restent enfermés dans
un intervalle limité est appelé ensemble de Julia. Il existe un nombre
infini d'ensembles de Julia dans la mesure où l'on peut donner au nombre
complexe c n'importe quelle valeur. Selon la valeur de c, l'ensemble de Julia
peut dessiner des figures très banales ou, au contraire, des images extraordinairement
complexes et souvent très esthétiques. Point fondamental ces ensembles de Julia
sont des structures fractales.
e) Obtention de nos fractales
Après avoir appliqué ces calculs, voici les superbes fractales que nous avons obtenues au bout de 1, 50 puis 200 itérations: